How To Generate Random Data In Sql Server

By: | Updated: 2020-04-01 | Comments (1) | Related: More > Functions System

Trouble

In this tip we look at different examples of getting random values using the SQL Server RAND function to give you a better thought of how this works and when and how to use information technology.

Solution

The SQL Server RAND role allows you to generate a pseudo-random sequence of numbers. The Microsoft SQL Docs site presents basic examples illustrating how to invoke the role. A pseudo-random sequence is one that is determined according to precise rules, only which appears to exist random. The values are often uniformly random over some range of values. The SQL Server RAND role generates pseudo-random numbers of this sort. MSSQLTips.com offers several prior tips comparing the RAND function to other ways of generating pseudo-random sequences and demonstrating extensions to the RAND function (here, here, and here). This tip focuses on the basics of how to invoke the function particularly highlighting the part of seed values forth with coordinated demonstrations.

Basic Operation of the RAND function

The RAND function operates with or without the specification of a seed value that tin can make up one's mind the ability to echo a sequence of output values. With or without a seed, the part returns a value from 0 through 1, exclusive. The return type from the function has a float information type. If the seed value is identical for successive invocations of the function, then the return value is the same for each successive run of the function. Seed values tin can have any of the post-obit 3 data types: tinyint, smallint, int. If you practise non specify a seed when invoking the part, then a random seed value is assigned in the background for each invocation of the function.

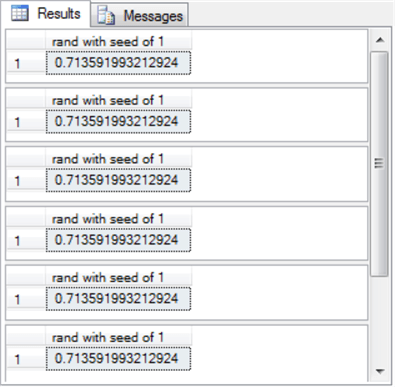
The following example shows the syntax for running the role 6 successive times with the same seed value (ane) for each invocation.

-- initial run select rand(1) [rand with seed of 1]   -- rand with same seed select rand(one) [rand with seed of 1]   -- rand with same seed select rand(1) [rand with seed of i]   -- rand with same seed select rand(1) [rand with seed of i]   -- rand with aforementioned seed select rand(1) [rand with seed of 1]   -- rand with same seed select rand(ane) [rand with seed of 1]

The output from the preceding script shows the returned values. Each return value is the aforementioned because each select argument relies on the same seed value of one. The function'southward output appears as a bladder value (0.713…).

Rand Syntax and Uses fig_1

If you lot specify a seed value just for the initial invocation of the RAND function and follow that past 5 more invocations of the role without a seed, so you tin can call up a repeatable list of pseudo-random values. The listing is repeatable in the sense that re-running a script returns the same list of pseudo-random values.

Here'southward a script that shows an initial RAND role invocation with the aforementioned seed as in the preceding script. However, the initial invocation is followed by five boosted RAND functions invocations without a seed value.

-- initial run select rand(1) [rand with seed of ane]   select rand() [start run of rand without seed]   select rand() [second run of rand without seed]   select rand() [tertiary run of rand without seed]   select rand() [fourth run of rand without seed]   select rand() [fifth run of rand without seed]

The following tabular array shows the results sets from ii sequent runs of the preceding script. Notice that each run returns the exact aforementioned sequence of values. This output confirms that the listing output by the script repeats the same sequence of pseudo-random values. The characteristic keeping the results the same beyond sequent runs is the seed value for the starting time invocation of the RAND part. If y'all modify the seed value for the initial invocation of the RAND function, then the pseudo-random sequence in the results set as well changes.

Results fix from commencement run of preceding script	Results set from 2d run of preceding script

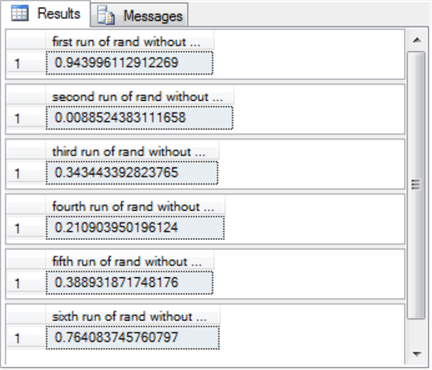
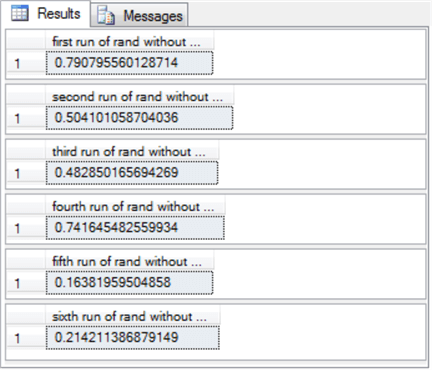
The next script shows vi sequent invocations of the RAND function, just this script does non specify a seed value for the initial function invocation nor any of the other invocations. When you do not specify a seed value, SQL Server automatically assigns a random value in the background. Therefore, each invocation returns a listing of half dozen pseudo-random values, simply the listing does not repeat beyond successive runs of the script.

-- initial run with no seed value select rand() [first run of rand without seed]  select rand() [2d run of rand without seed]  select rand() [third run of rand without seed]  select rand() [fourth run of rand without seed]  select rand() [5th run of rand without seed]  select rand() [sixth run of rand without seed]

Here's the output from ii consecutive runs of the preceding script. Detect the results sets are different beyond consecutive runs. The list of pseudo-random numbers in each list are unique considering there is no user-supplied seed value for the initial invocation of the RAND role.

Results set from starting time run of preceding script	Results prepare from second run of preceding script

Generating a uniform distribution of random digits

Past default, the RAND function returns values with a uniform distribution. By a uniform distribution, it is meant the frequency is the same across discrete pseudo-random values as well as beyond continuous pseudo-random value ranges with the aforementioned width. Furthermore, SQL developers can transform the uniform float values from the RAND function to discrete values, such every bit the integer values of one through ten. This section demonstrates the code for accomplishing this kind of transformation for RAND function output. In addition, this department examines the pseudo-random digit output from a script to confirm that the counts for the ten digits is approximately the same beyond successive script runs.

Hither'due south the script to create a fresh version of a table for storing randomly created digits, populating the tabular array with 1 thousand digits, and and then counting the frequency of occurrence of each digit value in the set.

The script starts with a block of code to drib any prior version of the #rand_digits tabular array. This is the tabular array that stores the one thousand digits created by a transformation of the output from the RAND function.
- A effort block followed by a catch block conditionally drops the #rand_digits tabular array. If the table does not exist already, a message is printed in the SQL Server Management Studio Letters tab indicating the table is not available to drib.
- Side by side, a create table statement creates a fresh re-create of rand_digits. The tabular array has i column named rand_digit with a tinyint data type.
The adjacent lawmaking cake declares and populates some local variables to manage the operation of the residuum of the script block.
- The @min_integer and @max_integer local variables specify the minimum and maximum integer value to be randomly generated. The script in this demonstration transforms the bladder values returned by the RAND role into integers in the range of one through ten.
- The @loop_ctr and @max_loop_ctr local variables facilitate the command of how many passes to perform through a while loop. Each pass through the loop generates and stores a successive random number.
  - The @loop_ctr variable starts with a value of zero.
  - On each successive pass through a while loop, the value of @loop_ctr is incremented by ane.
  - When @loop_ctr equals the value of @max_loop_ctr, the script transfers control to the first statement after the loop.
The next cake of code transforms bladder values returned by the RAND part to digits from one through x. In add-on, on each pass through the loop, the randomly created digit based on the output of the RAND function is inserted into the #rand_digits table.
- Begin and end statements circumscribe the code to be executed on each pass through the while loop.
- The select argument following an insert statement in the while loop transforms the bladder values generated by the RAND function to integers from one through 10. Past re-specifying the values for @min_integer and @max_integer too equally perhaps their data type, you tin designate whatever other minimum and maximum values your requirements dictate.
- After a random digit is inserted into #rand_digits, a fix statement increments the value of @loop_ctr past ane.
The final block of lawmaking in the script counts each digit created by the ane grand passes through the while loop.
- A select statement groups the rows by rand_digit values.
- The cavalcade of count office values is assigned the alias frequency.
- An guild past clause arranges the output from the select argument in ascending order past rand_digit value.

-- This code sample returns a uniform distribution of  -- digits from @min_integer (1) through @max_integer (x)   -- create a fresh copy of #rand_digits begin try drib tabular array #rand_digits finish try brainstorm take hold of    impress '#rand_digits not available to drop' cease take hold of   create table #rand_digits ( rand_digit tinyint )   -- declare min and max random digit values -- and variables values to control loop count declare   @min_integer tinyint =   1 ,@max_integer tinyint =  10 ,@loop_ctr int = 0 ,@max_loop_ctr int = 1000   -- loop thousand times  while @loop_ctr < @max_loop_ctr begin   -- generate a random digit from @min_integer through @max_integer -- and insert information technology into #rand_digits  insert #rand_digits(rand_digit) select floor(rand()*(@max_integer - @min_integer + 1) + @min_integer)   set @loop_ctr = @loop_ctr + 1   end   -- count the number of each randomly computed digit -- and display the results select rand_digit, count(*) [frequency] from #rand_digits group by rand_digit club past rand_digit

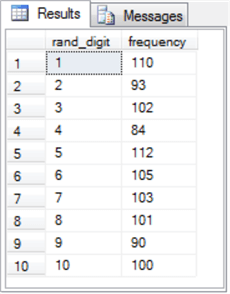
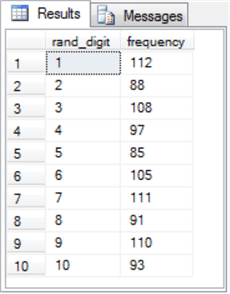
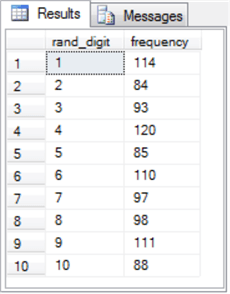
The post-obit tabular array shows the results sets from three sequent runs of the preceding script.

Discover that each results ready has rand_digit and frequency columns.
The rand_digit column values extend from one through 10 in each results set.
The frequency column values vary from one results gear up to the next. However, you can meet that the frequency column values are around 100 for each row. This effect indicates the frequency values are approximately uniformly distributed within each of the three results sets.
The frequency column values are distinct considering the pseudo-rand values generated from each run of the script is unique even while their distribution overall reflects a uniform distribution.

Pseudo-random digit values that are uniformly distributed offer many potential benefits to database applications, including taking a random sample of the rows in a very big table. The next department illustrates one approach to implementing this kind of solution.

Results set from 1 ^st Script Run	Results set from 2 ^nd Script Run	Results set from 3 ^rd Script Run

Selecting a random sample from a very big tabular array

Two prior tips demonstrated how to create a data warehouse of historical stock prices and volumes with data from the first trading date in 2009 through October 7, 2019. The Next Steps section in this tip contains links for learning more about the data warehouse. A fact table in the data warehouse (yahoo_prices_valid_vols_only) contains over fourteen million rows. Earlier demonstrating random sampling techniques for rows from a large tabular array, it volition exist helpful to query the yahoo_prices_valid_vols_only tabular array to get together a few metrics on its contents. The following script generates these metrics.

Not only does the following script compute the metrics, but it also creates a temporary table (#symbols_with_all_dates) with a subset of the stock symbols from the information warehouse. The temporary table stores a subset of symbols from the information warehouse with a distinct symbol_id integer value for each symbol.

The script starts by creating a fresh copy of the tabular array (#symbols_with_all_dates).
Next, the script reveals the exact number of rows in the fact table (14,620,885).
So, the script shows the total number of symbols in the fact table (viii,089).
This is followed past another select statement that counts the number of distinct trading dates in the fact table (2709).
Stock markets regularly annals new stocks for trading too as drop existing stocks that are no longer traded. The side by side query finds a subset of symbols that has a appointment value for all the distinct trading dates in the information warehouse. The row_number role in a query assigns a symbol_id value to each such symbol. At that place are 2,614 symbols in the subset. This subset populates the #symbols_with_all_dates table.
The final select statement in the script displays the rows in #symbols_with_all_dates.

begin attempt    drop tabular array #symbols_with_all_dates end attempt begin grab    print '#symbols_with_all_dates not available to driblet' end catch go   -- number of rows (fourteen,620,885) in the yahoo_prices_valid_vols_only table select count(*) [number of rows] from for_csv_from_python.[dbo].[yahoo_prices_valid_vols_only]   -- 8089 symbols select count(distinct symbol) distinct_symbol_count from for_csv_from_python.[dbo].[yahoo_prices_valid_vols_only]   -- 2709 trading dates select count(distinct [date]) distinct_date_count from for_csv_from_python.[dbo].[yahoo_prices_valid_vols_only]   -- 2614 symbols accept all trading dates (2709) select row_number() over (order past symbol) symbol_id, symbol into #symbols_with_all_dates from for_csv_from_python.[dbo].[yahoo_prices_valid_vols_only] group by symbol having count([close]) = ( -- 2709 trading dates select count(distinct [appointment]) distinct_date_count from for_csv_from_python.[dbo].[yahoo_prices_valid_vols_only] )   -- display contents of #symbols_with_all_dates select * from #symbols_with_all_dates order by symbol

Starting with #symbols_with_all_dates and yahoo_prices_valid_vols_only, the next script demonstrates how to draw two different random samples each having ten symbols from the distinct symbols in #symbols_with_all_dates. There are seven,081,326 rows in the target population from which sampling is performed. These rows are derived for toll and volume information for each of 2614 symbols for 2709 trading dates.

There are 2 major code blocks in the script beneath. The first code block is for drawing a random sample for the first prepare of ten symbols. The second lawmaking block is for drawing a sample for the 2d set of ten symbols. Each cake of code commences with a pair of header annotate lines cogent the code as for the kickoff or second sample.

The script begins by creating a fresh copy and populating the #sample_1_of_symbols table. The 2nd code cake creates a fresh copy and populates the #sample_2_of_symbols table. Both major code blocks conclude by displaying data for kickoff and last trading date for each symbol in its sample.
The code block for each sample uses a different seed value for the initial RAND function invocation that specifies its symbols.
- The seed value for the start sample is 1.
- The seed value for the 2d sample is 2.
- The pseudo-random digits for each sample are in the range from 1 through 2,614. Each digit corresponds to a singled-out symbol. The symbols are stored in #sample_1_of_symbols for the first sample and #sample_2_of_symbols for the 2nd sample.
The concluding 2 select statements in each major lawmaking block displays the prices and volumes for each sample of symbols. These select statements draw on yahoo_prices_valid_vols_only and either #sample_1_of_symbols or #sample_2_of_symbols.
- The starting time select statement displays data for the first trading date.
- The 2nd select statement displays data for the last trading date.

The preceding script displays iv results sets – two for the first sample and two more for the 2nd sample. The structure of the pair of results sets for each sample is the aforementioned. Therefore, the following screen shot shows just the two results sets for the beginning sample. Additionally, all four results sets are displayed later in an Excel worksheet and discussed from an analytical perspective.

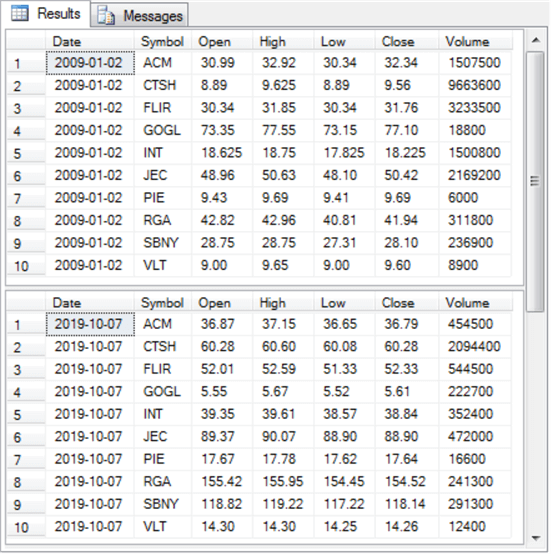
The adjacent two screen shots display results sets for the first sample from SQL Server Management Studio.

Each results set has iii types of information.
- The get-go type includes two columns, Engagement and Symbol, that identify each row by a trading appointment and a symbol.
- The 2nd type of data includes 4 types of prices.
  - The close price is critical in that it reveals the price for a stock at the end of a trading date.
  - The other three prices convey some feel for the path of a stock's toll during a trading appointment on its way to the close toll.
    - The open up cost shows the price at the open of a trading engagement.
    - The high and the depression prices indicate, respectively, the pinnacle and the bottom prices on a trading engagement.
- The third type of data is in the Book cavalcade. This indicates the number of shares exchanged during a trading date. Generally, analysts ascribe more than significance to prices during a trading appointment when the volume is significantly above boilerplate.
The beginning results set for the offset sample appears on superlative. This results set shows the 3 types of information for the first trading date for each of the symbols belonging to the commencement sample.
The second results set for the first sample appears on the bottom in the screen shot below. This results set displays the iii types of data for the last trading date for each of the symbols belonging to the first sample.

Rand Syntax and Uses fig_9

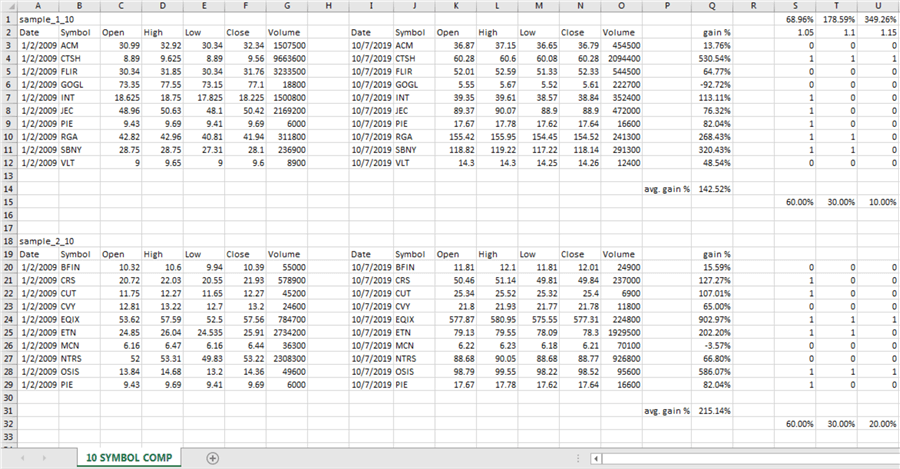
The next screen shot is for an Excel spreadsheet showing a pair of results sets for each sample.

The showtime and second results sets for the first sample appear, respectively, in rows 3 through 12.
- The first results prepare for the first trading date (1/2/2009) appears in columns A through M.
- The second results set for the final trading date (10/vii/2019) appears in columns I through O.
The first and 2nd results sets for the second sample appears, respectively, in rows twenty through 29.
- Again, the starting time results prepare for the showtime trading date (1/2/2009) appears in columns A through Thou.
- Also, the 2nd results set for the last trading date (10/vii/2019) appears in columns I through O.
The symbols for each sample are listed in alphabetical order in column B.
- The first symbol in the kickoff sample is ACM, and the last symbol in the beginning sample is VLT.
- The first symbol in the second sample is BFIN, and the terminal symbol in the second sample is PIE.

Several analyses follow to assistance identify if and how the ii unlike samples confirm they are from the same population of cost and volume data because they yield similar results.

Cell Q14 is the average percent gain betwixt the first and last close price across the 10 symbols in the first sample. Therefore, the average close price proceeds for the outset sample is slightly greater than 142 percent. The comparable price gain for the 2d sample (run into cell Q31) is slightly more than 215 percent. Considering of the disparity in average close price proceeds percent values, it is not obvious that both samples are from the same population.
Columns S, T, and U prove a different kind of comparison betwixt the ii samples.
- The values in column S for rows 3 through 12 in the first sample and rows xx through 29 in the second sample are
  - i when the percent gain is greater than five percent per year for the terminal close price relative to the first close price
  - 0 when the last close price is not five pct greater per year than the first close toll
- The 0's and 1'southward in column T are assigned as
  - one when the concluding shut price is more than x per centum greater per year than the first close price
  - 0 when the last close price is not more than 10 percent greater per twelvemonth than the first shut price
- The cutting-off value for beingness one in column U is more than fifteen percent greater per year (and 0 otherwise).
The results across all the symbols are summarized in row 15 for the first sample and in row 32 for the second sample. As you can see, the percent greater than a criterion value is very like beyond the 2 samples.
- Both the five percent per year and x percent per year comparisons are exactly the same at
  - 60% for more than than the 5 percent per twelvemonth comparing
  - 30% for the more than than ten percent per year comparison
- In general, y'all tin can come across there is a tendency for the percent greater than a benchmark value to reject as the criterion value rises. This general tendency continues through the fifteen pct per year criterion, just the proportion of sample symbols is not exactly the same betwixt the two samples: x percentage for the first sample and 20 percent for the second sample.

Rand Syntax and Uses fig_10

The preceding analyses in this department are simply a pick of examples for assessing if and how 2 samples from the same underlying population yield comparable results. Every bit this section confirms, the assessment nigh if two samples are similar depends on how you compare them. Therefore, y'all should tailor your comparisons based on the needs of those requiring the results.

Next Steps

The T-SQL scripts and worksheets for information displays and analyses are available in this tip's download file. After you confirm that you lot are getting valid results with the code from the download file, try variations to T-SQL code from this tip.

Yous can re-run the second script in the offset department with dissimilar seed values to confirm that pseudo-random sequences depend on the seed value for the RAND function.
Yous can also change the assignments for the @min_integer and @max_integer local variables for the script for the "Generating a uniform distribution of random digits" section. These changes will let y'all to confirm your ability to command the minimum and maximum pseudo-random values generated by a RAND part.

If you desire to test the code for this tip's terminal department, then you besides need to run scripts from Collecting Time Serial Information for Stock Market with SQL Server and Time Series Data Fact and Dimension Tables for SQL Server. Scripts from these ii prior tips will re-create the yahoo_prices_valid_vols_only table in your SQL Server example. You lot can draw different samples of symbols from those in the last section by specifying different seed values for the initial RAND function invocations.

Of course, the best way to derive value from this tip is past running the code in the download for this tip with your company's data. If y'all encounter issues, I look forward to answering any questions that you lot take near how the code should piece of work and/or how to get the code to piece of work for your personal needs.